Quantitative Planet:Teaching General Education Math for Non-Science Majors in a Geoscience Department

KEELY A. O'FARRELL (k.ofarrell@uky.edu) is an assistant professor in the Department of Earth and Environmental Sciences, University of Kentucky, Lexington, KY. REBECCA L. FREEMAN (rebecca. freeman@uky.edu) is an assistant professor and associate chair in the Department of Earth and Environmental Sciences, University of Kentucky, Lexington, KY.

Geoscience departments have long offered introductory courses ranging from standard (physical geology) to exotic (dinosaurs and disasters). Although these courses are primarily for non-science majors, they serve as recruiting tools in a discipline initially chosen by few students (Hoisch and Bowie, 2011). At the University of Kentucky (UK), general education curriculum changes led to required fields of inquiry through courses not tied to individual departments or colleges, but to fulfillment of learning outcomes. Our geoscience department unexpectedly found itself competing over "Intellectual Inquiry in the Natural, Physical, and Mathematical Sciences," as colleges ranging from Fine Arts to Public Health added new courses — "Physics of Music" and "Disease Detectives," among other catchy titles. However, perhaps demonstrating that faculty as well as students suffer from "math anxiety," "Quantitative Foundations" remained primarily an offering of basic algebra or calculus courses. We recognized the opportunity to expand offerings through a geoscience content-focused algebra and trigonometry course.

Admittedly, the initial idea for this course was prompted by a changing budgetary landscape and a desire for derrieres behind the desks, but we quickly realized that the pedagogical literature supported us, and that many existing geoscience exercises could be adapted for our purposes (for example: Earth's Interior Structure - Seismic Travel Times in a Constant Velocity Sphere, and Hotspots and Plate Motion) Geoscience has emphasized quantitative skills in introductory courses to improve quantitative literacy and to change public perception of the discipline as primarily qualitative (Manduca et al., 2008). Geology traditionally emphasizes quantitative reasoning along with quantitative literacy (Powell and Leveson, 2004) and is therefore an appropriate venue for providing a broad basic quantitative skill set.

Other institutions have introduced interdisciplinary science approaches to teaching algebra. One study resulted in improved college students' attitudes about math and enhanced their critical thinking skills, but did not result in significant improvement in math skills over a control group enrolled in a more traditional algebra course (Elliott et al., 2001). More recently, an integrated approach to teaching undergraduate algebra through chemistry and physics improved students' confidence and attitudes towards math (Dame et al., 2018).

At UK, the university-mandated learning outcomes for "Quantitative Foundations" are two-fold and perfectly aligned with geological practices. Students 1) demonstrate proficiency with number sense, identify functional relationships between variables, and relate different representations of these relationships and 2) apply these elements to solve problems drawn from real life.

×

Provenance: Department Chair David Moecher conceived of the idea and wrote several exercises used in this course. KEELY A. O’FARRELL (k.ofarrell@uky.edu) is an assistant professor in the Department of Earth and Environmental Sciences, Univer- sity of Kentucky, Lexington, KY. REBECCA L. FREEMAN (rebecca. freeman@uky.edu) is an assistant professor and associate chair in the Department of Earth and Environmental Sciences, University of Kentucky, Lexington, KY.
Reuse: This item is offered under a Creative Commons Attribution-NonCommercial-ShareAlike license http://creativecommons.org/licenses/by-nc-sa/3.0/ You may reuse this item for non-commercial purposes as long as you provide attribution and offer any derivative works under a similar license.

The newly developed interdisciplinary course, "Quantitative Planet," is taught by simultaneously introducing geologic concepts and basic math skills. See example exercises on page 7 and in Appendix 1 (the ONLINE EXTRAS). A discussion of our planet's place in the Solar System introduces students to triangulation and parallax, as they determine the distance to distant planets. This exercise also introduces the concept of error as the students see that small errors lead to wildly different results. Follow-up homework requires the use of triangulation or other methods discussed in class to measure the height of the tallest campus building.

×

Provenance: Department Chair David Moecher conceived of the idea and wrote several exercises used in this course KEELY A. O’FARRELL (k.ofarrell@uky.edu) is an assistant professor in the Department of Earth and Environmental Sciences, Univer- sity of Kentucky, Lexington, KY. REBECCA L. FREEMAN (rebecca. freeman@uky.edu) is an assistant professor and associate chair in the Department of Earth and Environmental Sciences, University of Kentucky, Lexington, KY.
Reuse: This item is offered under a Creative Commons Attribution-NonCommercial-ShareAlike license http://creativecommons.org/licenses/by-nc-sa/3.0/ You may reuse this item for non-commercial purposes as long as you provide attribution and offer any derivative works under a similar license.

Radioactive decay provides a natural topic for a section of the course, along with an opportunity to introduce geology's signature combination of quantitative reasoning and literacy as students must put their calculated ages into context through working out the sequence of events for a cross-section. The decay equation introduces students to more complicated math than they might see in a basic intro algebra course. To overcome this challenge, the equation is introduced and students learn two methods to solve it.

First, students "guess and check" by assuming a time for their sample daughter-parent ratio and seeing if the equation gives them the same (ratio) answer. Once this concept is mastered, the mathematical solution to the decay equation introduces students to logarithms and exponents as they learn how to find an exact age of a rock sample by solving the decay equation. Further exercises require using both methods to determine which gives a better result.

Additional examples of incorporating math into geologic topics include learning about plate motion to introduce simple ways to calculate velocity and examining earthquake locations to provide an opportunity to plot data and interpret trends.

The twice-weekly 75-minute class periods devote at least half of class time to working through problem sets with the help of the instructor and a teaching assistant in a class of 30–40 students. Some of this formative assessment is graded and some is simply reviewed. Frequent testing improves learning in algebra courses (Kika et al., 1992), especially for struggling students and the "testing effect" (Roediger and Karpicke, 2006) works even when exercises are not graded, as long as feedback is provided (Butler and Roediger, 2008). Encouraging practice in a low-stakes supportive environment is an important component of teaching math through encouraging a "growth mindset" (Yorke and Knight, 2008), the idea that you can be good at something if you practice, rather than the fixed mindset of "I'm just not good at math" that many non-science majors have adopted during their K–12 years. To address these concerns, exercises each week include variations on problems shown in class from the current lecture and recent past lectures to encourage lots of practice of quantitative skills. The students report feeling that their math skills improved over the course of the class.

×

(Above) A graph of student learning outcomes over the three semesters Quantitative Planet course was taught. Scores go from 1 (strongly disagree) to 5 (strongly agree). A majority of outcomes reported the same or higher scores each subsequent year.

Provenance: KEELY A. O’FARRELL (k.ofarrell@uky.edu) is an assistant professor in the Department of Earth and Environmental Sciences, Univer- sity of Kentucky, Lexington, KY. REBECCA L. FREEMAN (rebecca. freeman@uky.edu) is an assistant professor and associate chair in the Department of Earth and Environmental Sciences, University of Kentucky, Lexington, KY.
Reuse: This item is offered under a Creative Commons Attribution-NonCommercial-ShareAlike license http://creativecommons.org/licenses/by-nc-sa/3.0/ You may reuse this item for non-commercial purposes as long as you provide attribution and offer any derivative works under a similar license.

To ease test anxiety for the mid-semester summative assessments, exams include all formulas used in class, and students are allowed to write any additional material that they wish to use during the exam on a single 3" x 5" card. These three exams, worth only 30% of the overall grade, include both quantitative problems and geologic qualitative logic. Students report that being able to demonstrate learning in multiple ways reduced anxiety over the quantitative aspects of exams. Feedback included: "Professor broke down math in a way that was easy to understand." "I liked actually applying the material to Earth– related problem sets. This assisted with my engagement because it heightened my interest and I knew why I was doing the material I was taught. I additionally liked the group projects for socialization reasons." Students are asked at the end of the year if they feel their math skills improved as a result of the course, and between 60% and 90% of students agreed that they were more comfortable with math at the end of the course.

The second learning outcome for this area of inquiry, assessed at a university-wide level, requires application of skills learned to real life. While the geoscience-centered design of the course embeds this outcome, assessment mandates an artifact. Students produce a final report and presentation that utilizes earthquake occurrence data available through the website of the Incorporated Research Institutions for Seismology (https://www.iris.edu/hq/). Groups of students choose regions and do statistical analyses of various aspects of earthquake occurrence (depth, frequency, size, etc.) in their area using Excel. They also relate the earthquakes to tectonic settings, producing an integrated report. Presentations provide feedback from fellow students before groups turn in final reports.

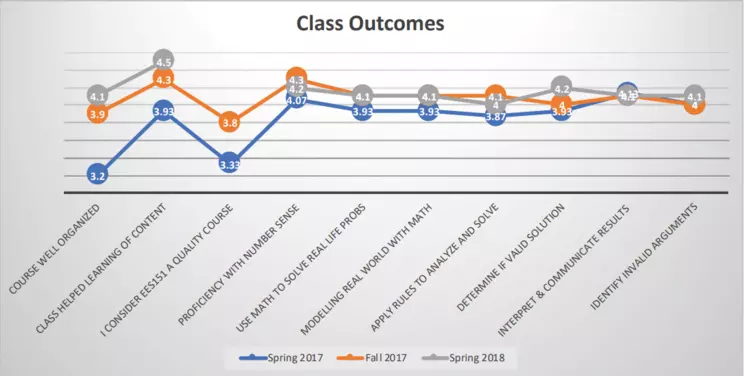
Modifications over three iterations led to better outcomes both in student learning and satisfaction (see graph above). For success in integrating geoscience and math, we urge others who adapt this model to review the wide body of literature on how people learn science as well as on how students learn math specifically. See Appendix 2 (ONLINE EXTRAS) for an annotated bibliography.

Finally, while beneficial impacts on student learning and perceptions of our discipline are laudable goals, teaching an algebra course through a geoscience department offers another deeply practical advantage. Geoscience departments are often smaller than other STEM departments and may be targeted during budget cuts. Generating student hours is essential to a college or university. Geoscience is not mandatory and competes with other science courses. But algebra generally is required as a terminal math course for non-science majors. Offering such a course provides justification to keep small geoscience programs and to support staffing hires.

Integrative approaches to STEM education demonstrably improve student attitudes towards math. Basic math and an understanding of how Earth works are essential science literacy skills. Combining geoscience content with math skills offers a pathway to better-prepared citizens as well as potential justification for the continued existence of geoscience departments.

ACKNOWLEDGEMENTS

Department Chair David Moecher conceived of the idea and wrote several exercises used in this course.

REFERENCES

Butler, A.C., and Roediger, H.L. III, 2008, Feedback enhances the positive effects and reduces the negative effects of multiple-choice testing: Memory and Cognition, v. 36, p. 604–616.

Dame, L., Aryal, B., Huq, A., and Prat-Resina, X., 2018, An interdisciplinary approach to connecting quantitative and science curricula and pedagogy in an undergraduate program: PRIMUS (just-accepted), p. 1–38.

Elliott, B., Oty, K., McArthur, J., and Clark, B., 2001, The effect of an interdisciplinary algebra/science course on students' problem solving skills, critical thinking skills and attitudes towards mathematics: International Journal of Mathematical Education in Science and Technology, v. 32, p. 811–816.

Hoisch, T.D., and Bowie, J.I., 2010, Assessing factors that influence the recruitment of majors from introductory geology classes at Northern Arizona University: Journal of Geoscience Education, v. 58, p. 166–176.

Kika, F.M., McLaughlin, T.F., and Dixon, J., 1992, Effects of frequent testing of secondary algebra students: The Journal of Educational Research, v. 85, p. 159–162.

Manduca, C.A., Baer, E., Hancock, G., Macdonald, R.H., Patterson, S., Savina, M., and Wenner, J., 2008, Making undergraduate geoscience quantitative: Eos, Transactions American Geophysical Union, v. 89, p. 149–150.

Powell, W., and Leveson, D., 2004, The unique role of introductory geology courses in teaching quantitative reasoning: Journal of Geoscience Education, v. 52, p. 301–305.

Roediger, H.L., and Karpicke, J.D., 2006, The power of testing memory: basic research and implications for educational practice: Perspectives on Psychological Science, v. 1, p. 181–210.

Yorke, M., and Knight, P., 2008, Self theories: some implications for teaching and learning in higher education: Studies in Higher Education, v. 29, p. 25–37.

Online Extras

PDF versions of the Homework

OFarrell andFreeman EES 151_homework1_edit.pdf (Acrobat (PDF) 98kB Jan24 20)

OFarrell andFreeman EES 151_homework2_edit.pdf (Acrobat (PDF) 62kB Jan22 20)

OFarrell and Freeman_EES 151_homework3.pdf (Acrobat (PDF) 95kB Jan24 20)

Annotated Bibliography

OFarrell and Freeman_online reference resources.docx (Microsoft Word 2007 (.docx) 18kB Jan24 20)